Jean Abraham dit Launay est un mathématicien né à Angers au XVIème siècle. Professeur ès Arts d’arithmétique et géométrie, il était arpenteur en Anjou. En 1605, Jean Abraham publie l’ouvrage qui est parvenu jusqu’à notre siècle [1]. On connaît assez peu de choses sur l’auteur. Cet ouvrage, réédité à plusieurs reprises jusqu’en 1645, est le seul à pouvoir nous faire découvrir ce mathématicien. Il est aussi le témoin de l’état des connaissances et des modes d’investigation de l’époque. C’est en 1839 que M. Huttemin, Professeur d’histoire naturelle au collège royal d’Angers, en fait une analyse critique sous forme d’une notice [2].
L’ouvrage et son rayonnement

L’ouvrage débute par une espitre dédicatoire à l’attention de Guillaume de Rosmadec, vicomte de Mayneuf (1542-1608), et suivi par un sonnet adressé au même seigneur. Deux sonnets sont ensuite adressés à Jean Abraham par Morelles Angeuin et La Touche Quilien Breton. L’ensemble du texte est parfois entrecoupé de quelques vers de l’auteur de l’ouvrage. Jean Abraham s’est donc essayé à la poésie sans toutefois en avoir obtenu une notoriété. A contrario, les nombreuses rééditions de ce livre témoignent de la diffusion de son œuvre en son temps, bien que là non-plus la célébrité à terme ne semble l’avoir atteint. Divers points se détachent du document :
- On peut y lire l’avancement des méthodes de calcul enseignées au XVIIème siècle et comprendre les objectifs de l’ouvrage.
- Ce document est également un témoin de la vie de tous les jours en ce siècle : le commerce, les modes de communication, les conflits, l’impôt…
- La référence à l’Anjou y est fréquente. Les lieux de cette région sont principalement évoqués pour servir de scène aux divers exercices proposés.
Un pédagogue avant tout
Ce document pédagogique comporte de multiples points d’intérêt. Une grande partie de ce livre est consacrée à l’arithmétique. On y trouve en premier lieu les méthodes pour effectuer les quatre opérations : addition, soustraction, multiplication et division. On y retrouve même nos tables de multiplications ! On y enseigne la preuve par 9 et la preuve par 7, mais aussi la règle de trois. On apprend à extraire les racines carrées. Tout ceci est validé par de multiples exemples présentés sous forme de plus de cent exercices de la vie courante de l’époque. Les exercices d’arithmétique proposés trouvent principalement leur application dans la conversion des unités de mesures entre régions, que ce soit pour la monnaie, pour la pesée, les distances, les volumes.
« Combien valent de livres 1234 deniers parce que la livre vaut 240 deniers qui font 24 dizaines, trenchez la derniere figure, & du reste prenez le quart du sixiéme pour avoir 5 livres, 2 sols, 10 deniers. »
La deuxième partie est consacrée à l’arpentage et à la géométrie en application à l’arpentage, cœur de métier de l’auteur hormis l’enseignement des mathématiques. L’auteur propose de multiples exemples de mesures de surfaces qu’il décompose en surfaces élémentaires comme on le ferait aujourd’hui.
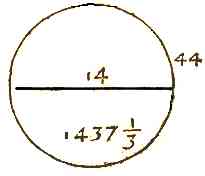
Le souci de la rigueur mathématique dans le calcul n’est pas prioritaire puisque l’auteur utilise l’approximation de Pi par 22/7 pour le calcul de surface de cercle et de volume de sphère qu’il appelle le « rond » et le « contenu du globe rond ou boule ronde ».
Or on sait que le mathématicien Viète (1540-1603) a déjà déterminé les 35 premières décimales de Pi. Les calculs de l’auteur sont en fait effectués en tant qu’arpenteur plutôt que mathématicien et de ce point de vue, l’approximation de Pi à 22/7 est largement satisfaisante.
La figure 2, extraite de l’ouvrage indique le calcul de la circonférence (C = 22/7 x 14 = 44) d’un cercle et du volume (V = 4/3 x 22/7 x 73 = 1437 1/3) d’une sphère de diamètres (D = 14) avec cette approximation .
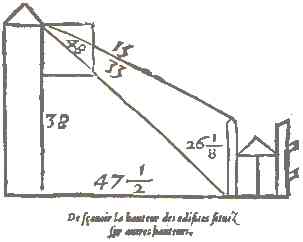
Les deux dernières parties (Géométrie inaccessible, toise des bâtiments, fabrication et usage des cadrans solaires) sont consacrées à l’exploitation des outils précédents. Les méthodes de mesure des bâtiments exposées ne sont pas novatrices (figure 3).
L’utilisation du quadrant nouveau et du carré d’ombres par exemple ont anticipé depuis bien longtemps ces modes opératoires [3]. Bien entendu, la fabrication de cadrans solaires est ancestrale et les explications de l’auteur ne semblent pas apporter de point de vue réellement novateur.
L’auteur évoque en fin d’ouvrage l’influence des phases de la lune sur les marées. Il donne une méthode pour déterminer l’âge de la lune, question dont on se préoccupait depuis bien longtemps [3]. Il ressort de tous ces points que l’ouvrage est avant tout pédagogique. Ceci est conforté par le fait qu’il ait été réédité pendant longtemps. C’est sans nul doute à l’époque un ouvrage de grand intérêt pour l’éducation et pour l’application aux domaines techniques exploités par l’auteur. Cet ouvrage est aussi destiné à revendiquer l’utilisation de l’arithmétique au détriment du comptage par jetons dans le cadre de plusieurs professions du commerce et des finances. L’auteur écrit en effet dans un paragraphe intitulé « De la difference du calcul ou supputation qui se fait par la plume ou par les gets » : « Ceux qui n’ont la cognoissance ou l’intelligence de l’Arithmetique, ignorent l’asseurance du calcul d’iceluy ». « … que le calcul fait avecques la plume est plus prompt & plus certain que celuy fait avecques les gettons … ».
Ces phrases signifient que l’un des objectifs de l’ouvrage est d’encourager l’utilisation de l’arithmétique (utilisation, par exemple de la preuve par 9 pour valider le résultat d’un calcul) au détriment du calcul par jetons.
Notre mathématicien angevin est probablement novateur en pédagogie, exprimant une évolution nécessaire au mode de calcul. Il est sans doute un bon pédagogue de son époque.
Un témoin de son temps
La lecture des énoncés proposés par l’auteur nous éclaire sur la vie de la fin du XVIème siècle et le début du suivant : Les échanges de marchandises, une économie basée essentiellement sur les produits agricoles (blé, céréales de tous types), l’évocation des conflits armés et du siège de villes : « L’on fait achapt de 25 pieces de marchandise, pour la somme de 59l. 4s. 2d [livres, sols, deniers] à la mesme raison combien valent 150.
Nous sommes aussi témoins, par ces récits de la difficulté qu’engendrait l’utilisation des unités : prix et mesure des volumes de grain par exemple : non uniformité de ces unités de mesure sur toutes les provinces qui est mise en évidence à plusieurs reprises dans des exercices de conversion. De nombreux exemples de mise en application des quatre opérations et de la règle de trois sont pris à propos des batailles militaires et concernent l’approvisionnement et la distribution de vivres et de vin pour les troupes. Les sièges de cités sont évoqués à plusieurs reprises : « Dans une ville assiegee il y a 458 soldats ou gens de guerre, qui n’ont que 12 pipes de vin, qu’il faut si bien gouverner que chacun d’iceux en ait chacun jour autant l’un que l’autre par le temps de 15 jours, que l’on espere que le siege se pourra lever. La pipe vaut 240 pots, le pot deux pintes, la pinte deux chopines…»
A la lecture de ces textes, il se dégage l’idée que ces événements faisaient partie du quotidien ou tout au moins étaient récurrents dans la vie des populations.
Un natif d’Angers
Jean Abraham a sans nul doute parcouru de nombreuses contrées, évoquant la latitude des villes de Rennes, Nantes, Paris, Rouen, Bourges, Lyon, Marseille, Nerbonne, Tholose, Bayonne & Aix, Bordeaux & Sainctes. Dans l’un de ses textes, l’auteur évoque explicitement sa présence à Rennes le 13 juin 1603 où il mesure la latitude de cette ville (48°17’). On peut supposer qu’il y a souvent séjourné. Indéniablement, il y loge en 1607, comme en témoigne la dernière phrase de l’épître qu’il adresse à Guillaume de Rosmadec :« A Rennes en Bretaigne, le dernier jour d’Avril, 1607 ».
Lors de l’évocation de sa tâche d’arpenteur, Jean Abraham écrit le 12 Janvier 1604 qu’il s’est rendu sur un terrain nommé « le Buzard » situé en la paroisse de « Sainte Jeanne » sur « … un bout de chemin tendant d’Angers à Chaudefons » :
« Premierement j’ay mesuré une piece de terre vulgairement appellee le Buzard, situee en ladite paroisse joignant d’un coste la terre de François Guerin, d’autre coste le pré de Jacques le Mesle, & d’un bout de chemin rendant d’Angers à Chaudefons. »
Les allusions qu’il fait à la région angevine, à travers ses sujets d’exercices d’arithmétique, de géométrie ou d’arpentage, sont fréquentes :
- « L’on a envoyé un messager d’Angers à Lyon, au temps que les jours ont 14 heures, faisant son voyage allant & venant il a esté 18 jours 5 heures, sçavoir lors que les jours auront 18 heures. Combien il sera de temps à faire ledit voyage. »
- « Le roy mande imposer sur ledit pays d’Anjou 1545 escus, le departement fait sur les villes dudit pays, la ville de Bauge est chargee de cent vingt sept escus, les essayeurs des paroisses dudit Bauge veulent sçavoir combien il faut imposer sur les taillables pour raison des escus sols & deniers que chacun d’eux a cy devant payé en la grand taille derniere qui se monte 358 escus. »
- « Si les 12 boisseaux mesure des ponts de See ou charge de cheval sont estimez valoir 14 1/3 boisseau mesure d’Orleans, sçavoir combien les 558 1/4 boisseau à la mesure d’Orleans valent à la mesure des ponts de See. »
- « Si le boisseau de la Val est plus de 1/6 que celuy d’Angers, celuy d’Angers est vendu 12 s.1/3, à tel prix, combien pourront valoir 100 boisseaux de la Val. »
- « Le septier de bled contenant 12 boisseaux à la mesure des ponts de See, les Angers fait la charge de cheval et la mine de bled contenant 8 boisseaux à la mesure de Rennes…. »
En conclusion
Notre étude de l’ouvrage de Jean Abraham permet de percevoir la pédagogie de l’auteur et faire apparaître quelques éléments du quotidien de l’époque. Né à Angers, l’auteur a exercé son métier d’arpenteur en Anjou, affirmant la nécessité de la connaissance et du développement de l’arithmétique et de la géométrie en application à l’arpentage. Il a sans doute sensibiliser ses contemporains avertis sur les méthodes de calcul et a dû contribuer à faciliter les conversions de mesures nécessaires dans le commerce. Au siècle suivant, le mathématicien Barrême publiera un ouvrage sur les mêmes thèmes. On y voit alors une progression en quantité d’informations et qualité d’impression de l’ouvrage [4].
Bibliographie :
[1] « Arpentage universel ; géométrie inaccessible, toise des bastimens, la fabrique & usage des quadrans sollaires & autre geometrie par la reigle &le compas », Jean Abraham, dit Launay, 1605 à 1645, Nicolas Loyselet, Rouen. Edition de 1635 :
[2] « Mémoires de la société d’agriculture, sciences et arts d’Angers, 4ème Volume, 1ère livraison », pp 54-62, 1839, Victor Pavie, Angers.
[3] « Le quadrant nouveau d’Angers » Marc Bourcerie, AMOPA, décembre 2021.
[4] « Le Livre facile pour apprendre l’arithmétique de soy-même & sans maître » François Barrême, 1736.
Article de Marc Bourcerie
Marc Bourcerie est professeur des universités honoraire. Il a enseigné à l’Université d’Angers, à Polytech Angers (ex ISTIA) et à l’IUT. Il est membre du bureau de l’AMOPA de Maine-et-Loire et officier des Palmes académiques.
Site AMOPA 49 : https://amopa49.fr/